Objetivo:
Explicar como o de-surveying funciona em Leapfrog Geo, Works y Geothermal.
Resolução:
Drillhole de-surveying é uma parte importante da construção do modelo e pode impactar significativamente no volume calculado das unidades geológicas modeladas. Na sua forma mais simples, o problema do drillhole de-surveying é encontrar o caminho mais razoável que sabemos entre:
- Inicio do survey
- Posição Inicial
- Fim do survey
- as distâncias entre as posições de inicio e final
Dadas as informações limitadas, há um grande número de caminhos que o furo poderia percorrer entre as medidas de survey, mas, dadas as restrições físicas impostas pela perfuração, os caminhos mais suaves são mais prováveis.
Há uma grande variedade de algoritmos disponíveis com uma variedade de nomes confusos. O Leapfrog implementa 3 algoritmos diferentes.
1. O algoritmo tangente básico. Ele assume que os furos (drilholes) mantenham a direção dada pela última medida de survey até encontrar uma nova medição.
Isso implica que o furo (drillhole) faz saltos agudos na direção sempre que existe uma medição. Isso parece bastante improvável, exceto quando o poço de perfuração é de fato uma trincheira. Em vez desse ser o procedimento padrão, o Leapfrog permite que os usuários identifiquem as posições de collar que se referem a trincheiras, para que esse algoritmo substitua o algoritmo padrão.
2. O arco esférico ou algoritmo de curvatura mínima (spherical arc or minimum curvature algorithm)
Essa é a explicação mais simples que se encaixa nos fatos. O algoritmo encaixa exatamente o survey nas posições inicial e final, e a curvatura é constante entre essas duas medidas. Nos pontos de survey a direção permanece contínua, portanto não há mudanças bruscas e irreais na direção.
Este é o algoritmo padrão do Leapfrog, e as distâncias downhole são desurveyed exatamente como as distâncias ao longo de um arco circular.
3. O algoritmo tangente balanceado (Balanced tangent algorithm)
Esse ainda utiliza linhas retas, mas tenta melhorar a precisão do algoritmo tangente atribuindo peso igual às medições de survey inicial e final. É uma melhoria no algoritmo tangente básico, mas ainda sofre com uma descontinuidade irrealista no caminho da perfuração. Dito isto, é uma melhor aproximação ao caminho geral da perfuração.
Então, qual é o melhor?
No Leapfrog, recomendamos como padrão o método de arco esférico (spherical arc method), porque ele modela os dados disponíveis da maneira mais simples e consistente com os fatos. Um fator importante é que muitos pacotes de software permitem ao usuário interpolar as medições da pesquisa para reduzir o tamanho dos segmentos de linha reta e criar um caminho mais suave. Se você usar segmentos muito pequenos, os resultados se aproximam do arco esférico padrão usado pelo Leapfrog.
Os erros aumentam com o aumento de curvatura; portanto, os erros serão pequenos para furos (drillholes) que são aproximadamente retos/menos curvos.
Então, por que o Leapfrog fornece o algoritmo de tangente balanceado (Balanced tangent algorithm) se não é tão bom?
Eventualmente, o usuário terá wireframes ou modelos que foram criados com os métodos tangentes em outros pacotes. Não é prático refazer grande parte deste trabalho, e a necessidade de ser consistente é mais importante que a precisão.
Sobre a importação:
Quando importamos o banco de dados de sondagem, o Leapfrog trabalha com o algoritmo de curvatura mínima como padrão.
Caso deseje modificar para o algoritmo tangente balanceado, dê um duplo clique no objeto survey na árvore de projeto. A opção abaixo vai aparecer e você pode escolher:
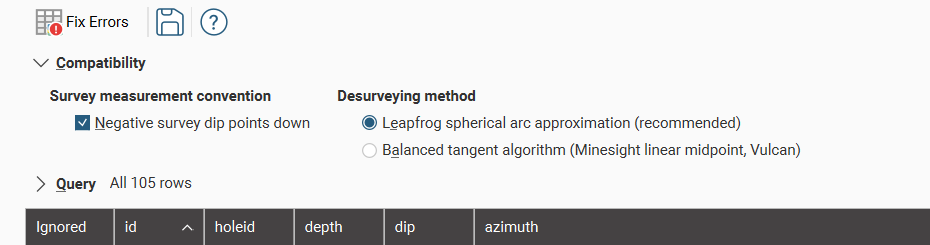
Caso deseje trabalhar com a opção do raw algorithm (algoritmo tangente básico), geralmente usado para trincheiras, dê um duplo clique no objeto collar e marque a coluna trench: