Drillhole de-surveying is an important part of model building and can impacts significantly on the volume of the calculated geological units. In its simplest form the problem of drillhole de-surveying is one of finding the most reasonable path where we know:
- the starting survey
- the starting position
- the end survey
- distance between the start and end
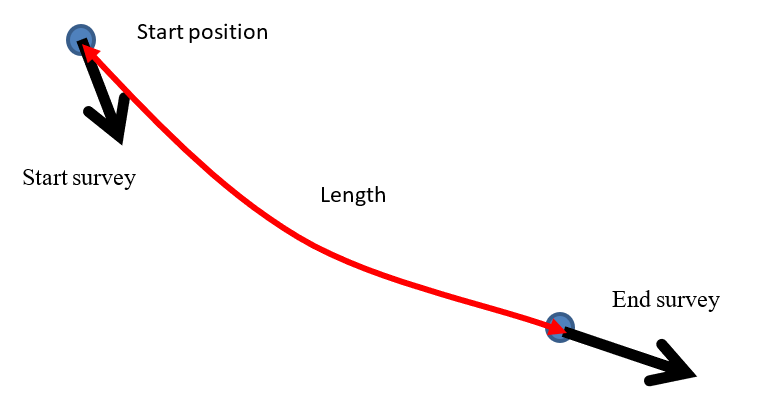
Given the limited information there are a large number of paths the drillhole could take between the survey measurements but given the physical constraints imposed by a drilling, the smoother paths are more likely.
There are a large variety of algorithms available with a variety of confusing names. Leapfrog implements 3 different algorithms.
1. The basic tangent algorithm. This assumes the drillhole maintains the direction given by the last survey measurement until it encounters a new measurement.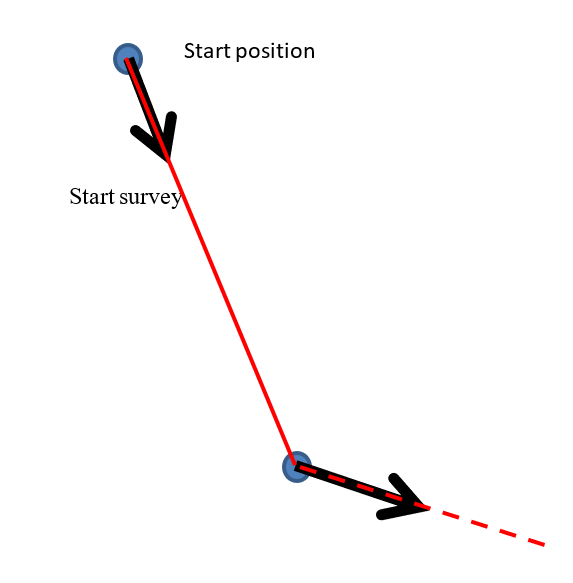
This implies that the drillhole makes sharp jumps in direction whenever a measurement is taken. This seems quite unlikely, except when the drillhole is in fact a trench. Rather than this make a general option, Leapfrog allows users to identify collar positions that refer to trenches when this algorithm overrides the standard algorithm.
2. The spherical arc or minimum curvature algorithm.
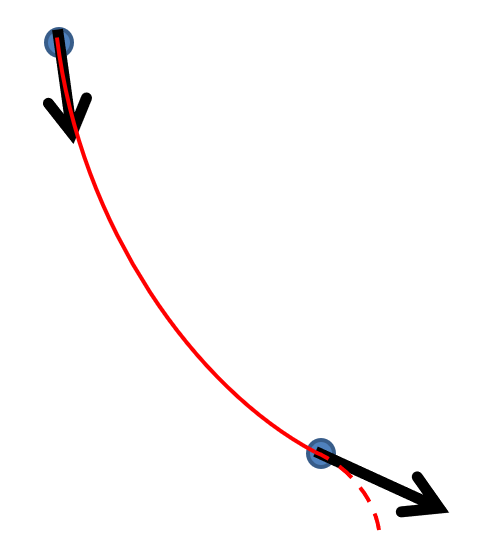
This is the simplest explanation that fits the facts. It matches the survey at the starting and end positions exactly and the curvature is constant between these two measurements. At the survey points the direction remains continuous, so there are no unrealistic sharp changes in direction.
This is the default algorithm in Leapfrog, and downhole distances are desurveyed exactly as distances along a circular arc.
3. The Balanced tangent algorithm
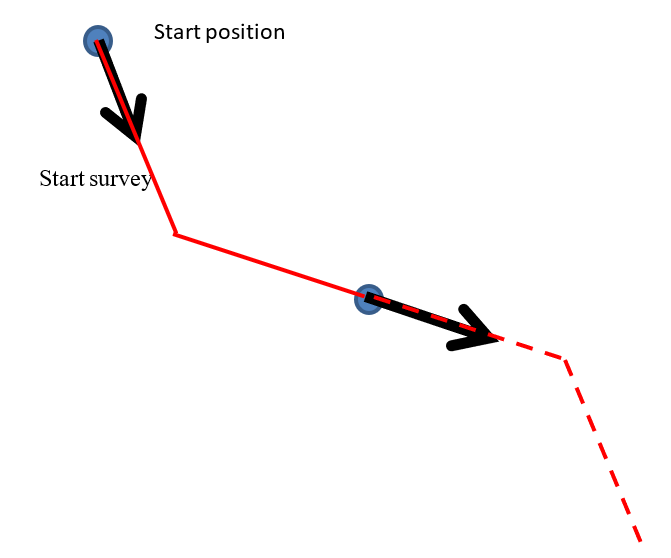
This still uses straight lines, but attempts to improve the accuracy of the tangent algorithm by assigning equal weight to the starting and end survey measurements. It’s an improvement on the raw tangent algorithm but still suffers from an unrealistic discontinuity in the drillhole path. That said it’s a better approximation to the overall drillhole path.
So which is best?
At Leapfrog we recommended default is the spherical arc method because it models the available data in the simplest manner consistent with the facts. A telling factor is that many software packages allow the user to interpolate the survey measurements to reduce the size of straight line segments and create a smoother path. If you use very small segments the results approach the default spherical arc used by Leapfrog.
The errors increase with the amount of curvature, so the errors will be small for drillholes that are approximately straight.
So why does Leapfrog 2.5 provide the balanced tangent algorithm if it’s not so good?
Often the user will have wireframes or models that have been created with the tangent methods in other packages. It’s not practical to redo much of this work and the need to be consistent is more important than accuracy.